2147. Number of Ways to Divide a Long Corridor #2535
-
|
Topics: Along a long library corridor, there is a line of seats and decorative plants. You are given a 0-indexed string One room divider has already been installed to the left of index Divide the corridor into non-overlapping sections, where each section has exactly two seats with any number of plants. There may be multiple ways to perform the division. Two ways are different if there is a position with a room divider installed in the first way but not in the second way. Return the number of ways to divide the corridor. Since the answer may be very large, return it modulo Example 1:
Example 2:
Example 3:
Constraints:
Hint:
|
Beta Was this translation helpful? Give feedback.
Replies: 1 comment 2 replies
-
|
We are given a corridor represented as a string of seats ( The goal is to count the number of valid ways to place dividers. A section can have any number of plants, but must have exactly 2 seats. Two ways are different if there's at least one position where a divider is placed in one way but not the other. Key Observations
Step-by-step ReasoningLet's walk through the example:
General Pattern
Special Cases
Mathematical FormulationFor
Let's implement this solution in PHP: 2147. Number of Ways to Divide a Long Corridor <?php
/**
* @param String $corridor
* @return Integer
*/
function numberOfWays($corridor) {
$MOD = 1000000007;
$n = strlen($corridor);
// Collect all seat indices
$seatIndices = [];
for ($i = 0; $i < $n; $i++) {
if ($corridor[$i] === 'S') {
$seatIndices[] = $i;
}
}
$seatCount = count($seatIndices);
// If no seats or odd number of seats, no valid division
if ($seatCount === 0 || $seatCount % 2 !== 0) {
return 0;
}
$ways = 1;
// For each gap between sections
for ($i = 2; $i < $seatCount; $i += 2) {
// Number of positions for divider between sections
$gap = $seatIndices[$i] - $seatIndices[$i - 1];
$ways = ($ways * $gap) % $MOD;
}
return $ways;
}
// Test cases
echo numberOfWays("SSPPSPS") . "\n"; // Output: 3
echo numberOfWays("PPSPSP") . "\n"; // Output: 1
echo numberOfWays("S") . "\n"; // Output: 0
?>Explanation:
Complexity
|
Beta Was this translation helpful? Give feedback.
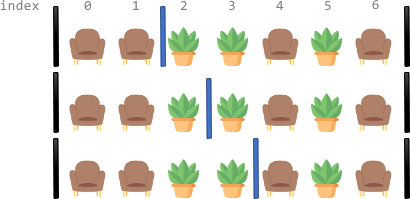

We are given a corridor represented as a string of seats (
'S') and plants ('P'). We need to divide it into sections such that each section has exactly 2 seats. There are already fixed dividers at the start and end. We can place additional dividers between any two adjacent positions (between indices i-1 and i).The goal is to count the number of valid ways to place dividers. A section can have any number of plants, but must have exactly 2 seats. Two ways are different if there's at least one position where a divider is placed in one way but not the other.
Key Observations